TEOREMA DE PITÁGORAS 

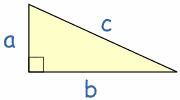
En un triángulo rectángulo el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los otros dos lados (llamamos "triángulo rectángulo" a un triángulo con un ángulo recto)

Entonces, el cuadrado de a (a²) más el cuadrado de b (b²) es igual al cuadrado de c (c²): a2 + b2 = c2

EJERCICIOS: 

1.- Encuentra el valor de la hipotenusa (c):

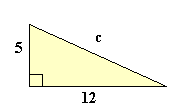
a² + b² = c²

5² + 12² = c²

25 + 144 = 169

c² = 169

c = √169

c = 13

2.- Hallar el valor de b:

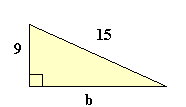
a² + b² = c²

9² + b² = 15²

81 + b² = 225

Resta 81 a ambos lados

b² = 144

b = √144

b = 12

TEOREMA DE TALES DE MILETO 

Como definición previa al enunciado del teorema, es necesario establecer que dos triángulos son semejantes si tienen los ángulos correspondientes iguales y sus lados son proporcionales entre si. El primer teorema de Tales recoge uno de los postulados más básicos de la geometría, a saber, que:

Si en un triángulo se traza una línea paralela a cualquiera de sus lados, se obtienen dos triángulos semejantes.

Entonces, veamos el primer Teorema de Tales en un triángulo:

Dado un triángulo ABC, si se traza un segmento paralelo, B'C', a uno de los lados del triángulo, se obtiene otro triángulo AB'C', cuyos lados son proporcionales a los del triángulo ABC. 

Lo que se traduce en la fórmula

 EJERCICIOS:

1.-Sabiendo que las rectas r, s y t son paralelas, la longitud de x es:

2.-Sabiendo que las rectas r, s y t son paralelas, las longitudes que faltan son: 

3.-Las rectas a, b y c son paralelas. Hallar la longitud de x.

 

 SEMEJANZA DE TRIÁNGULOS 

 Dos triángulos son semejantes si tienen dos ángulos iguales.

     

Dos triángulos son semejantes si tienen los lados proporcionales.

     

Dos triángulos son semejantes si tienen dos lados proporcionales y el ángulo comprendido entre ellos igual.

     

CONGRUENCIA DE TRIÁNGULOS 

Criterios de congruencia

Los criterios de congruencia corresponden a los postulados y teoremas que enuncian cuáles son las condiciones mínimas que deben reunir dos o más triángulos para que sean congruentes. 

Estas son:

1.- Congruencia de sus lados

2.- Congruencia de sus ángulos

Para que dos triángulos sean congruentes, es suficiente que sólo algunos lados y/o ángulos sean iguales.

Los postulados o criterios básicos de congruencia de triángulos son:

Postulado LAL

LAL significa lado-ángulo-lado.

Dos triángulos son congruentes si tienen dos lados y el ángulo determinado por ellos respectivamente iguales.

Postulado ALA

ALA significa ángulo-lado-ángulo.

Dos triángulos son congruentes si tienen dos ángulos y el lado común a ellos, respectivamente, iguales.

 

Postulado LAA 

Dos triángulos que tienen un lado, un ángulo adyacente y el ángulo opuesto a ese lado respectivamente congruentes, son congruentes.

Postulado LLL

LLL significa lado-lado-lado.

Dos triángulos son congruentes si tienen sus tres lados respectivamente iguales.

ÁNGULOS INTERIORES Y EXTERIORES DE UN TRIÁNGULO 

ÁNGULOS INTERNOS 

Un ángulo interior de un triángulo lo forman dos lados.

La suma de los ángulos interiores de un triángulo es igual a 180°.

A + B + C = 180º

ÁNGULOS EXTERNOS 

Un ángulo interior y exterior de un triángulo son suplementarios, es decir, suman 180º.

Los ángulos exteriores de un triángulo lo forman un lado y su prolongación.

 El valor de un ángulo exterior de un triángulo es igual a la suma de los dos interiores no adyacentes.

  Un ángulo interior y exterior de un triángulo son suplementarios, es decir, suman 180º.

α = 180º - A

ÁNGULOS ENTRE DOS PARALELAS Y UNA SECANTE 

Partiendo de dos rectas paralelas r y s, y una transversal t que corta a ambas, da lugar a ocho ángulos, cuya posición relativa da lugar a su definición.

Ángulos internos.

Se llaman ángulos internos a los que forman dos rectas cortadas por una secante y quedan entre las dos rectas.

Ángulos externos.

Reciben el nombre de ángulos externos los que forman dos rectas cortadas por una secante y quedan fuera de dichas rectas.

Ángulos correspondientes.

Son los ángulos situados al mismo lado de la secante y al mismo lado de las rectas cortadas por ésta, siendo uno de ellos interno y el otro externo. Cuando las dos rectas cortadas por la secante son paralelas, los ángulos correspondientes son iguales.

Ángulos alternos internos.

Son los formados por dos rectas cortadas por una secante, internos, no contíguos ni adyacentes, situados entre las dos rectas, a uno y otro lado de la secante. Si las dos rectas cortadas por la secante son paralelas, sus ángulos alternos internos son iguales.

TIPOS DE PARES DE ÁNGULOS

ÁNGULOS ADYACENTES

Son ángulos que tienen un lado común y los otros dos pertenecen a la misma recta.         

ÁNGULOS OPUESTOS AL VÉRTICE

Ángulos opuestos por el vértice son aquellos cuyos lados de uno son semirrectas opuestas a los lados del otro.
Los vértices de ambos ángulos son comunes y sus lados están en un par de rectas que se cortan en el vértice común, pero no poseen ningún punto interior común.

ÁNGULOS COMPLEMENTARIOS.-

Dos ángulos son complementarios si suman 90 grados (un ángulo recto). Estos dos ángulos (40° y 50°) son ángulos complementarios, porque suman 90°.

Fíjate en que juntos hacen un ángulo recto. Pero los ángulos no tienen por qué estar juntos. Estos dos son complementarios porque 27° + 63° = 90°

ÁNGULOS SUPLEMENTARIOS

Dos ángulos son suplementarios si suman 180 grados.
Estos dos ángulos (140° y 40°) son ángulos suplementarios, porque suman 180°.

Fíjate en que al ponerlos juntos tenemos un ángulo llano.

Pero no hace falta que los ángulos estén juntos.
Estos dos son suplementarios porque 60° + 120° = 180°